(xyz)^2 using suitable identity 2 See answers devansh00gupta devansh00gupta (xyz) ^2 = x^2 y^2z^22xy 2yz2zx SVBS SVBS X^2y^2z^22xy2yz2xz New questions in Math 2ncos =sin 40ncos40 the value of 1÷n² is a book is 5 cm thik and each cover is 15 mm thikhow thik is the book without its cover?Xy 2,z =hx,zihy,zi, 2 h(xy),zi =hx,zihy,zi, 3 hαx ,zi =αhx,zi for all α ∈ Q, 4 hαx ,zi =αhx,zi for all α ∈ R Details of the proof (not covered in lectures) are below 1The proof for F=Cproceeds in a similar way under the definition, for all x,y ∈ X hx,yi = 1The identity of indiscernibles is an ontological principle that states that there cannot be separate objects or entities that have all their properties in common That is, entities x and y are identical if every predicate possessed by x is also possessed by y and vice versa It states that no two distinct things (such as snowflakes) can be exactly alike, but this is intended as a metaphysical
1
What is the formula of (x+y+z)^3
What is the formula of (x+y+z)^3- (x^3y^3)=(xy)(x^2xyy^2) This is a sum of cubes This is a semiimportant identity to know (x^3y^3)=(xy)(x^2xyy^2) Although it doesn't apply directly to this question, it's also important to know that (x^3y^3)=(xy)(x^2xyy^2) This gives us the rule (x^3y^3)=(xy)(x^2∓xyy^2)Writing any polynomial directly just requires listing all possible exponent combinations of a^x*b^y*c^z where every term has xyz=3 and the coefficient of each term is (xyz)!/(x!y!z!) This works for any length polynomial and in this case we would have a^3 b^3 c



2
This video shows how to expand using the identity '(xy)3=x3y33x2y3xy2'To view more Educational content, please visit https//wwwyoutubecom/appuseriesaClick here👆to get an answer to your question ️ Factorise 27x^3 y^3 z^3 9xyz using identity Join / Login maths Factorise 2 7 x 3 y 3 z 3 − 9 x y z using identity Answer 2 7 xWhere i, j, k are the standard unit vectors for the x, y, zaxes Each arrow is labeled with the result of an identity, specifically, the result of applying the operator at the arrow's tail to the operator at its head The blue circle in the middle means curl of curl exists, whereas the other two red circles (dashed) mean that DD and GG do
This algebraic identity can be written in the following form too ( a − b) 3 = a 3 − b 3 − 3 a 2 b 3 a b 2 Generally, the a minus b whole cubed algebraic identity is called by the following three ways in mathematics The cube of difference between two terms identity or simply the cube of difference identity The cube of a binomial formulaAnswer 27x3 y3 z3 −9xyz = (3x)3 y3 z3 −9xyz = (3x)3 y3 z3 −3×3x×y×z using identity a3 b3 c3 −3abc = (abc)(a2 b2 c2 −ab−bc−ca) Putting a = 3x,b = y,c = z = (3xyz)(9x213 Identity and cardinality Two sets are identical if and only if 2 they have exactly the same members So A = B iff for every x, x ∈ A ⇔ x ∈ B For example, {0,2,4} = {x x is an even natural number less than 5} From the definition of identity follows that there exists only one empty set;
Using the identity and proof x^3 y^3 z^3 3xyz = (x y z) (x^2 y^2 z^2 xy yz zx)• R has a multiplicative identity element, often called 1 ie 8x 2R, 1 x = x 1 = x • R has the distributive laws 8x,y,z 2R, we have x (y z) = x y x z, (x y)z = x z y z A ring is a field F if multiplication is commutative and every nonzero element has a multiplicative Prove the identity x^3 y^3 z^3 2xyz = ( xyz) (x^2 y^2 z^2 xy yz XX) 2 See answers vsg4737 vsg4737 Using (x−y)2≥0(x−y)2≥0 one gets x2y2≥2xyx2y2≥2xy Since each xx, yy, and zz are positive, the following three equations can be obtained



1




How To Prepare Your Ecommerce Business For A Cookieless Future Via Sejournal Iambenwood Wp Guy News
Use the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^2−x^y−y^z−z^x) to determine the value of the sum of three integers given the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of any two products (xyyzzx) is 107(x1) (x2) = x 2 3x 2 Symmetric polynomial identities ( x, y, z) n in terms of σ 1 = x y z, σ 2 = x y y z x z and σ 3 = x y z In Arthur Engels "Problem Solving Strategies" book in the section on symmetric polynomials, he asks us to prove the identities below I read up on expanding trinomials and got the quickest method to be a variation on Pascal's triangle




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




X Y Z 3 Formula Novocom Top
Use the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^2−xy−yz−zx) to determine the value of the sum of three integers given the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of anyExpand (xyz)^2 Rewrite as Expand by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply by Rewrite using the commutative property of multiplication Multiply by Multiply by Multiply byPolynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2




A By Quest Journals Issuu



1
a b c = x 2 (eq1) a 2 b 2 c 2 = y 2 (eq2) a 3 b 3 c 3 = z 3 (eq3) The smallest in positive integers is M 1 = {1498, 2461, 7490}, so, 1498 2461 7490 = 107 2 1498 2 2461 2 7490 2 = 8025 2 1498 3 2461 3 7490 3 = 7597 3 There are also an infinite number of distinct Martin triples unscaled by a square factor, and this can be proved via a polynomial identityQuantum logic gates are represented by unitary matricesA gate which acts on qubits is represented by a unitary matrix, and the set of all such gates with the group operation of matrix multiplication is the symmetry group U(2 n)The quantum states that the gates act upon are unit vectors in complex dimensions, where the norm is the modulus squared The basis vectors areOn x^3 x y^3 y = z^3 z Suppose we wish to find an infinite set of solutions of the equation x^3 x y^3 y = z^3 z (1) where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and x=uv




X Y Z 3 Formula Novocom Top




Project 3 Identity Through Type Hurley Woodford
A classic way to prove inequalities is using AMGM inequality But my approach is different Here's my proof According to an algebraic identity, mathx^3 y^3 z^3 3xyz/math math= (xyz)(x^2y^2z^2xyyzzx)/math(1) As x, y & zBasic rotations A basic rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system The following three basic rotation matrices rotate vectors by an angle θ about the x, y, or zaxis, in three dimensions, using the righthand rule—which codifies their alternating signs (The same matrices can also represent a clockwise rotation of the axesThe algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra formulas for class 9, which are mathematical rule expressed in symbols but the algebraic identities represent that the equation is true for all the values of the variables For example;




V Boolean Algebra 1 Derive This Identity X X Y Chegg Com




Maths Identity 8 Polynomial Part 12 English Youtube
Use sum of cubes identity to find x3y3 z3 = (xy z)(x2y2 −xyz z2) We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3Answer x3 −8y3 −64z3 −24xyz = (x)3 (−2y)3 (−4z)3 −3(x)(−2y)(−4z) = (x−2y−4z)x2 (−2y)2 (−4z)2 −x(−2y)(−4z)−(−4z)x = (x−2y−4z)(x2 4y2 16z2 2xy−8yz4zx)




X Y Z 3 Identity Novocom Top




Ultimate Brand Creation Corporate Identity Case Study For Brand Identity Design Services Ppt Inspiration Background Images Pdf Powerpoint Templates
(xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) x3y3xy(12x2yy) y3z3yz(12y2zz) z3x3zx(12z2xx) = 3(xy)(yz)(zx) all the cubes then cancelxy(12x2yy) yz(12y2zz) zx(12z2xx) = 3(xy)(yz)(zx) Then I start to struggle toThe proofs of these are straightforward using su x or 'x y z' notation and follow from the fact that div and curl are linear operations 15 2 Product Laws Using identity (3), we have r 3(r r) = r 3 (rr) rr(r 3) 58 We have previously shown that rr= 3 and that r(rn) = nrn 2 r Hence r 3(r r) = r 3 (rr) rr(r 3) = 3 r3 r 3 r5 r = 3Get a quick overview of Algebraic Identity of (xy)³ and (xy)³ from More Complex Identities in just 3 minutes Algebraic Identities (xy)³ & (xy)³ Comparing the polynomial with the identity we have, x = 3 a & y = b Using the values of x & y, other terms of




General Relativity Solution Sheet 2



2
Take any Pythagorean triplet (a, b, c) Multiplying c6k − 2, where k is a natural number As an alternative, you can take any standard Pythagorean triple, eg 32 42 = 52, and then multiply through by 54 to get which will give an infinite set of solutions x = a3 − 3ab2, y = 3a2b − b3, zIdentity 1 curl grad U = 0 62 • U(x,y,z) is a scalar field Then ∇∇×∇ ∇U = ˆı ˆ ˆk ∂/∂x ∂/∂y ∂/∂z ∂U/∂x ∂U/∂y ∂U/∂z = ˆı ∂2U ∂y∂z − ∂2U ∂z∂y ˆ () ˆk() = 0 Now remember some of the games you can play with Boolean algebra, like wy = w (xx')y = wxy wx'y to generate terms that you need Your goal then is to start on one side and generate the terms on the other side In doing so, you will probably have to generate some additional terms that you don't want to survive




Pokemon The Series Xyz Wikipedia




Q 58 If X Y Z 0 Then X3 Y3 Z3 Equals 1 3 Xyz 2 2xy2z 3 Maths Linear Equations In Two Variables Meritnation Com
This easily follows from the FibonacciBrahmagupta identity (a 2 b 2) (c 2 d 2) = (a c b d) Hence, x 2 y 3 z ≤ 14 x 2y 3z \leq \sqrt{14} x 2 y 3 z ≤ 1 4 with equality holding when x 1 = y 2 = z 3 \frac{x}{1} = \frac{y}{2} = \frac{z}{3} 1 xX was not identical with both Y and Z, that is identical with the 5air It followed that Bombos could have no possible claim upon Y Here Bombos's lawyer spotted a weakness in Morion's case For, while it had to be conceded that X was not identical with each of Y and Z, it was not obvious that X could not be identical with the fair His3 Curl The curl of a vector field, F(x,y,z), in three dimensions may be written curlF(x,y,z) = ∇×F(x,y,z), ie ∇×F(x,y,z) = (∂F 3 ∂y − ∂F 2 ∂z)i−(∂F 3 ∂x − ∂F 1 ∂z)j (∂F 2 ∂x − ∂F 1 ∂y)k = i j k ∂ ∂x ∂ ∂y ∂ ∂z F 1 F 2 F 3 It is obtained by taking the vector product of the vector operator




8 3 Prove Algebraically The Following Identity X Yz Chegg Com



Www Topperlearning Com Answer Using Identities Prove That X Y Z 2 3 Xy Yz Zx Where X Y Z Are Positive Real Numbers 3gc3fduu
Since the identity is in terms of x, y, x, y, x, y, and z z z, collect like terms with these variables a x 3 5 y − c z 16 = 16 x 3 b y − 3 z d x 3 (a − 16) y (5 − b) − z (c − 3) (16 − d) = 0 \begin{aligned} ax^{3}5ycz16&=16x^{3}by3zd\\ x^{3}(a16)y(5b)z(c3)(16d)&=0 \end{aligned} a x 3 5 y − c z 1 6Solution Theorem 3 (a) and (b) THEOREM 3 (a) Law of Absorption yxx = x Proof yxx = yxx1 by identity (Ax 2b) = x (y1) by distributivity (Ax 4a) = x1 by Theorem 2 (a) = x by identity (Ax 2b) THEOREM 3 (b) x (xy) = x by duality Theorem 6 (a) and (b) THEOREM 6 (a) De Morgan's Laws (xy)' = x'y'If a, b, c, are integers (in the ring Z) then one has the discrete Heisenberg group H 3 (Z)It is a nonabelian nilpotent groupIt has two generators, = (), = and relations =, =, =, where = is the generator of the center of H 3 (Note that the inverses of x, y, and z replace the 1 above the diagonal with −1) By Bass's theorem, it has a polynomial growth rate of order 4




Use The Identity X A X B X 2




Tutorial Sheet 03 Phys Dynamics And Vector Calculus Studocu
Its identity is fully determined by its absence 10 A polynomial from Qx, y, z is a polynomial from Qx, yz, so it can be viewed as a polynomial in z with coefficients from the integral domain Qx, y p(z) = z3 − 3xy ⋅ z x3 y3 So we can try our methods to factor a polynomial of degree 3 over an integral domain If it can be factored then there is a factor of degree 1, we callThis video shows how to evaluate using the identity'x3y3z33xyz=(xyz)(x2y2z2xyyzzx)'To view more Educational content, please visit https//wwwyout
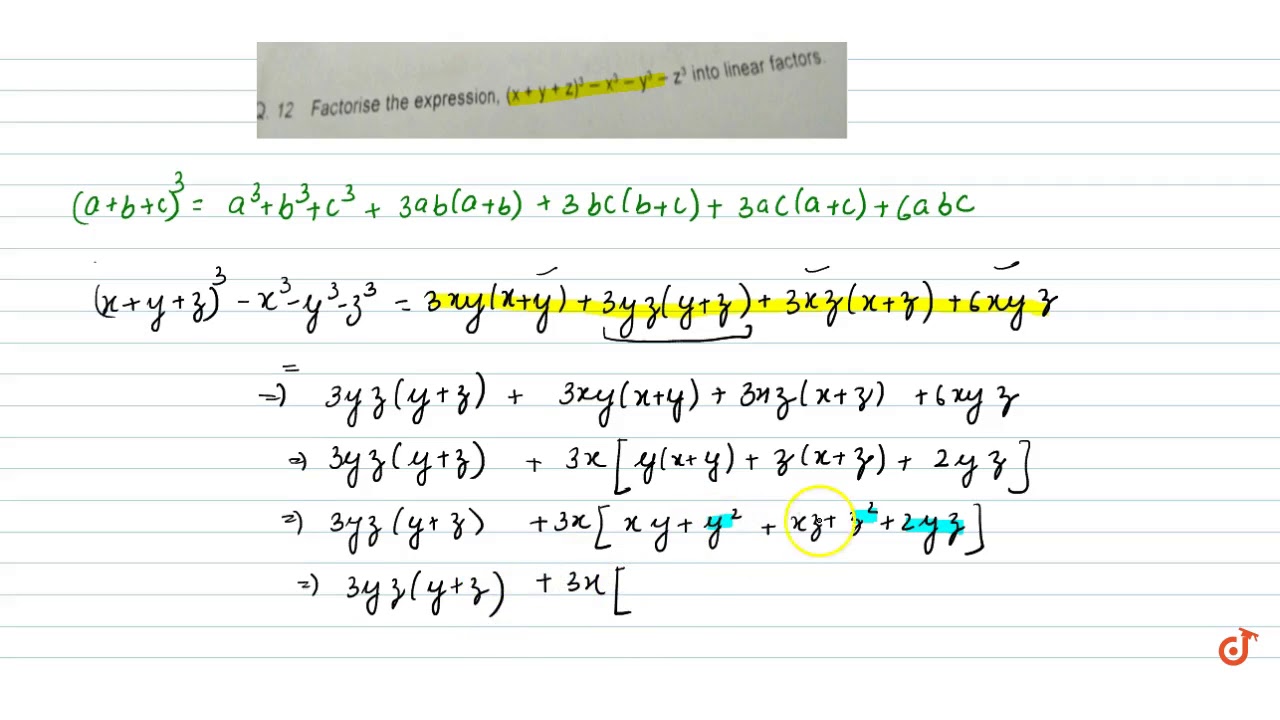



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube




Working With The Organization Chart Netiq Identity Manager User S Guide To The Identity Applications
By the way, my "Most Wanted" problem #16 asks if the equation x^3 y^3 z^3 = 1 has any algebraic solutions other than (1 9m^3)^3 (9m^4)^3 (9m^4 3m)^3 = 1 and, if so, whether ALL the integer solutions are given by such an algebraic identityThere are close connections between quaternion algebra and the algebra of vectors in 3dimensional space the components x, y and z of i, j and k respectively in the quaternion a xi yj zk can be thought of as the three components of a vector (x,y,z) in 3dimensional space, and the Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0




Entry 330 By Ammar619 For Corporate Identity For A Biotech Startup Freelancer




X Y Z 3 Identity Novocom Top
x n 3 y n 3 z n 3 = (− 1) n (For a proof, see JHHan and MDHirschhorn, "Another look at an amazing identity of Ramanujan", MathMag 79 (06), , or alternately either of two earlier papers by Hirschhorn cited in that one) 4 Answers4 det ( x y z y z x z x y) = 3 x y z − ( x 3 y 3 z 3) Let AMGM n stands for the statement of the arithmeticgeometric inequality in n variables A classical, elementary approach (due to Cauchy, Cours d'Analyse) is to show AMGM 2 ⊢ AMGM 4 ⊢ AMGM 3Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of a x and y In the activity method, the identities are verified by cutting and pasting paper




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




Rento Xyz Brand Identity Domestika




Identity Parameter An Overview Sciencedirect Topics




New Logo And Identity For Hemslojden By Snask Branding Search By Muzli




Formula




If X Y Z 0 Then Find The Value Of X 3 Y 3 Z 3 Maths Algebraic Expressions And Identities Meritnation Com




Xyz 4 Xyz 2 Use Identity Brainly In




Desidero Identity Redesign By Berkay Dace On Dribbble




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Ex 9 5 2 Use The Identity X A X B X 2 A B X Ab To



Insilico Xyz Identity



2




X Y Z 3 Identity Novocom Top




Aws Identity And Access Management Iam Aws For Industries




Find The Value Of X Cube Y Cube Z Cube Minus 3 X Y Z If X Square Y Square Z Square Is Equal To Brainly In




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Trigonometric Identities List Of Trigonometric Identities Examples




Personas Frequently Asked Questions Segment Documentation




X Y Z 3 Identity Novocom Top




Using Identities Prove That X Y Z 2 3 Xy Yz Zx Where X Y Z Are Positive Real Numbers Maths Polynomials Meritnation Com




X Y Z 3 Identity Novocom Top




Xyz Storage Identity
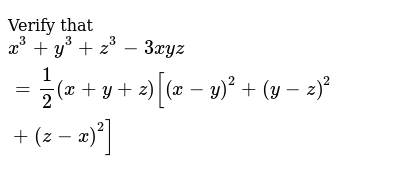



Verify That X Cube Y Cube Z Cube Minus 3 X Y Z Is Equal To On




Kickstart Visual Identity On Behance




Read Ansatsu Kyoushitsu Chapter 180 3 Extra 3 Identity Time Mangamad




Graduate Fashion Week




If X Y Z 1 Xy Yz Zx 1 Xyz 1 Find X 3 Y 3 Z 3




Solved 1 Construct A Truth Table For The Following A X Chegg Com




Update Column 1 Based On Time And Repeating Value In Column B Stack Overflow




11 Iii 5a 7 5a 7 1 2m 0 3 1 2m 0 3 Vii 6y




3 Ways To Create A Logo Design Xyz Domain Names Join Generation Xyz




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




Abstract S Brand Identity Online Shop Logo Vector Design Uplabs




What Is The Expansion Of A B C 3 Quora




Ex 9 5 2 Use The Identity X A X B X 2 A B X Ab To




Leveraging The Information Contained In Theory Presentations Springerlink



Enhancing Public Digital Identity System Spid To Prevent Information Leakage Springerlink




Rento Xyz Brand Identity Domestika
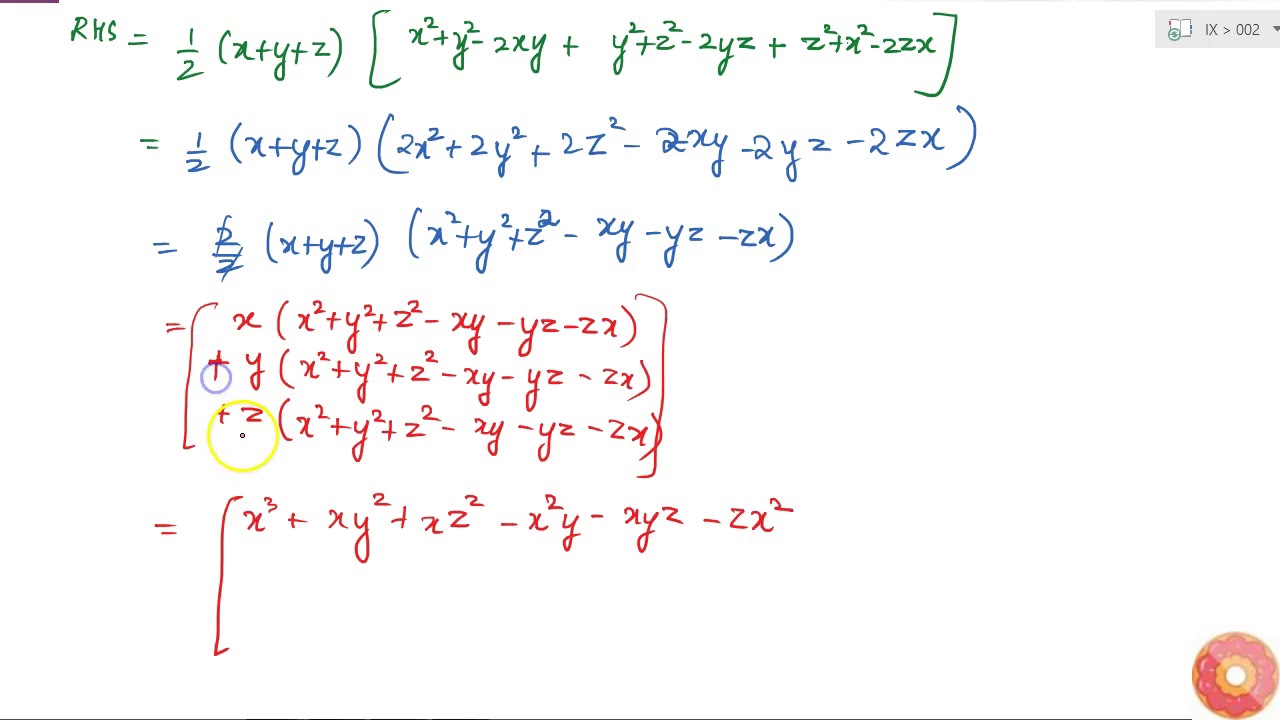



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Cbsetuts Com




3 10 Points Simplify The Following Functional Chegg Com




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



The Android Style Guide And Google S Emerging Identity Phonearena




Simple Semirings



How Digital Identity Protects Your Software Stack Overflow Blog




2 Simplify The Following Functional Expression And Chegg Com




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Exercise 6 3 Access Free Pdf




The Hepworth Prize For Sculpture On Behance Identity Design Logo Brand Identity Guidelines Branding Design




Polynomials Ppt Video Online Download




Veresaev Sergeyveresaev Www Hicetnunc Xyz Objkt Nitter Tweet View




Evolvit Brand Identity Guidelines By Nazmul Hossan On Dribbble



The Fig 1 Shows Ring Signature User Allocation System When User Logged Download Scientific Diagram




Pinniped Kubernetes Single Sign On With Openid Connect Linuxblog Xyz




Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5 And X 3 Y 3 Z 3 7 Then The Value Of X 4 Y 4 Z 4 Is




Ex10 Internet Standards Cyberspace




Pin On Reference




Pdf Leadership Storytelling Event As A Means Of Prompting Organizational Identity Change Semantic Scholar




A By Quest Journals Issuu




2x 3y 6z 10 2y 4z 40 X Y Z 10 Find The Mat Gauthmath




Adidas Company Brand Direction On Behance Beer Branding Design Identity Logo Corporate Design



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




How Do I Simplify F X Yz Xy Z Xyz Stack Overflow




X Y Z 3 Identity Novocom Top




Introduction To Robotics By Ed Red A Robot




My Brand Design Process Tina Perko Design




Symmetric Polynomial Identities X Y Z N In Terms Of Sigma 1 X Y Z Sigma 2 Xy Yz Xz And Sigma 3 Xyz Mathematics Stack Exchange



Www Mdpi Com 76 3417 11 7 3012 Pdf




Use The Identity X A X B X 2 A B X Ab To Find The Follow




Although You Answered My Question But I Cannot Understand The Answer So I Would Request You To Pls Answer Maths Polynomials Meritnation Com




Polkaproject T Co Dcw9dtnbuz Guide 008 Litentry Mathgiveaway 3 Dot To Winners Win At Random 1 Follow Polkaprojectcom And Litentry 2 3 Friends 3 Retweet Tracking Claim




Secureist Brand Identity Case Study On Behance




Vector Of Trendy Modern Alphabet Letters And Numbers Stock Illustration Download Image Now Istock




X Y Z 3 Identity Novocom Top




If X Y Z 0 Then Show That X Cube Y Cube Z Cube 3xyz Mathematics Topperlearning Com Vj2f0044




2x 3y 6z 10 2y 4z 40 X Y Z 10 Find The Mat Gauthmath
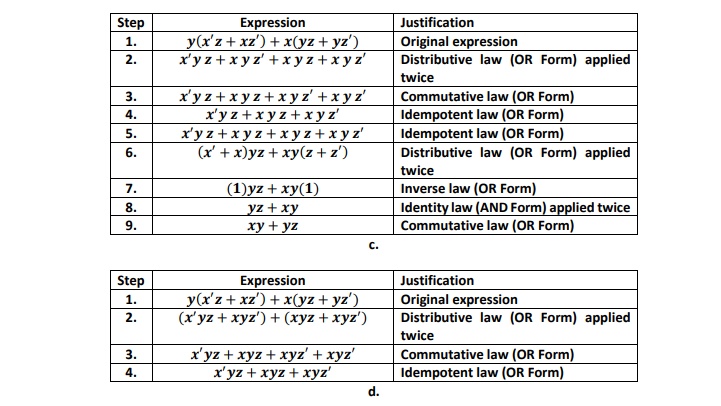



Solved 17 Determine Which One Of The Following Simplifi




Calculus 3 Divergence And Curl 31 Of 50 Identity 7 Curl Curl F Grad Div F Grad 2 F Youtube




X Y Z 3 Identity Novocom Top



0 件のコメント:
コメントを投稿